GPT编程01——翻转游戏

前言

GPT4-o的发行，标志着可用的大语言模型的进一步发展。现在，GPT在编程方面的能力已经很强了。这个系列将以GPT作为助手，基本使用GPT实现项目的需求，完成项目。与此同时辅以手动debug。
目前，我的期待是锻炼GPT编程水平，同时通过GPT给出的代码学习相关函数的使用，积累知识。

2405270859版本：修正代码块(之前用的不是反引号‘`’)；完善标题结构；注：output不是GPT的输出，是我自拟的表示该文件里有GPT当次回答所提供的代码。
2406111057版本：手机端代码块显示问题等待解决。修复演示程序中生成过随机题目后更改大小导致不合理版面的bug；给演示程序的源html加上了N范围为2~10的限制，防止标题以及按钮被覆盖。

Project_No1:Flip_Game 翻转问题->游戏交互

背景

翻转问题（亮灯问题），多次在解密游戏中碰到。十分有魅力。

需求

1. 基本实现界面，有重置、查看可行解的功能；
2. 可以给出具体N值时的特例，作为一道谜题；
3. 可以记录点击的步数；
4. 可以支持对同一道题的多次尝试，记录玩家的最优步数。

灵感列表：

1. 点击后，触发翻转事件的格子不是我点击的格子，该格子与我点击的格子沿水平中线对称（将直角坐标系移到中心后，两个格子关于x轴对称）。(要给操作上难度的确可以对称位置操作，竞速时倒可以作为干扰因素)
2. 可以添加选择渐变色的功能，给出几种选择。

提问->解析的形式

之前看过一篇对翻转问题进行分析的文章，文章中通过渐变色格子展示N*N时的最优解，很是壮观。因此，私心想用渐变色表示~~

渐变色表示与基本游戏逻辑实现

Q:使用python，画NN的方格，其中指定下标的方格为渐变颜色，其余为白色，有粗边框，方格间有细边框
A:当然可以！你可以使用Python的matplotlib库来画出这样的渐变色方格。下面是一个实现的示例代码：output:001.py
代码解释
导入必要的库：matplotlib.pyplot用于绘图，numpy用于处理数值数组，matplotlib.colors用于处理颜色。
创建绘图函数：draw_grid函数接收网格大小N和需要渐变颜色的方格坐标列表gradient_cells。
设置图像和轴：
关闭坐标轴刻度。
设置粗边框。
绘制NN网格：
使用双重循环创建方格。如果方格在gradient_cells中，则创建渐变颜色。否则，填充白色。
添加细边框：
使用循环和ax.plot函数添加细边框。
设置轴的限制和纵横比：
确保整个网格显示在图像中，并且每个方格都是正方形。
显示图像：使用plt.show()显示图像。
通过此代码，你可以生成一个包含渐变颜色和边框的NN网格。你可以根据需要调整渐变颜色和指定方格的坐标。
Q:如何设置渐变色？有什么已有的渐变色模板吗？
Q:其中有没有渐变色只有一种主色系的？ output:002.py
Q:有没有浅蓝到紫晶蓝的渐变色 output:003.py
Q:能否做一个翻转问题的界面，要求能与界面交互。界面大小为44，被翻转的为渐变色，未被翻转的为白色 output:004.py
Q:翻转问题，是翻转一个格子，上下左右的格子也会一并翻转的问题，当全部格子被翻面即成功。根据这个信息进行修改 output:005.py
Q:渐变色能不能由中心向外？ output:006.py
Q:那个格子自身也要翻转 output:007.py
Q:……
File “E:\Project_storage\方格.venv\Lib\site-packages\matplotlib\artist.py”, line 1011, in set_alpha
raise ValueError(f’alpha ({alpha}) is outside 0-1 range’)
ValueError: alpha (1.118033988749895) is outside 0-1 range
A:这个错误是因为尝试设置了超出范围的 alpha 值。我们需要确保 alpha 值在 0 到 1 的范围内。修改代码，使得 alpha 值不会超出这个范围。下面是修正后的代码：
output:008.py

对界面交互的修正

通过与界面进行交互，发现了几个问题：

1. 点击后，触发翻转事件的格子不是我点击的格子，该格子与我点击的格子沿水平中线对称（将直角坐标系移到中心后，两个格子关于x轴对称）。(要给操作上难度的确可以对称位置操作，竞速时倒可以作为干扰因素)
2. 触发事件的格子并没有翻转，但周围的格子的正常翻转了
3. 坐标为（3，3）的格子翻转状态无法正确显示，虽然边框好像会变
   

翻转的逻辑

Q:在def flip_tile(self, x, y):中，第一行的self.grid[y, x] = not self.grid[y, x]与后面的逻辑重复了，导致目标格子会被翻转两次，导致无法翻转。请自行修正。 另外，点击后，触发翻转事件的格子不是我点击的格子，该格子与我点击的格子沿水平中线对称（将直角坐标系移到中心后，两个格子关于x轴对称）。 此外，坐标为（3，3）的格子翻转状态无法正确显示。

把发现的错误讲给GPT后，GPT没能有效修正(009.py)，只能手动修正了。
手动修正，必须理解代码的运行逻辑。如果不理解代码，只能看着错误干瞪眼。还是对着008.py修改。
手动修正时，还是可以借助GPT理解各部分代码的，但要谨防瞎说，不确定得自行验证or查文档。

Q:……请解释这些代码

在我对着解释理解各句代码的作用并在对应位置写入注释时，突发奇想，GPT应该也能完成这种机械化工作吧。于是：

Q:能否讲你的解释，压缩后嵌入代码中？

GPT的确能做到，没问到的部分它也做出了解释，但这种提问的解释必定不细致。不过重要的是理解各个参数与函数是怎么用的。

经过测试，发现一个新的线索：目前的平面直角坐标系原点在左下角。这应该是坐标逻辑出错的原因。多半就是坐标确定的逻辑出错了。在自己手动修改前还是试试GPT在知道问题时能不能自己改吧。

Q:经过测试发现，目前的直角坐标系原点在左下角，导致格子的y坐标计算错误。请根据这个情况进行修正

010.py
的确修正了。但是现在点击格子之后，触发事件的格子会向上偏移。最后一行的格子甚至压根无法触发事件。照例先告诉GPT这个问题。

Q:现在点击格子之后，触发事件的格子会向上偏移。尤其是点击最后一行的格子时，触发的永远是倒数第二行的格子。

011.py
问题并没有得到解决，顺带一提，新加的坐标显示，左上角格子编号(0,0)。与刚才的左下是坐标原点的逻辑基础相违背。刚才列出的问题1、3都没有得到解决。再给GPT一次机会。分析主要抓住坐标的逻辑，难不成y上取整了？
坐标确定代码为：

x, y = int(event.xdata), int(self.N - event.ydata - 1)  # 获取点

跟上取整了差不多了，math.floor(N-y坐标-1)，第四行$$y \in (0,1)$$，所以$$(N-y-1) \in (2,3)$$，取下于它的最大整数（floor函数的功能）只能是2了，所以根本取不到最后一行(y=3)。
将int(self.N - event.ydata - 1)改为int(self.N - event.ydata)，逻辑就正确了。
把这个线索交给GPT，这是它最后的机会了。

Q:对于int(self.N - event.ydata - 1)，当y属于(0,1)时，好像int(self.N - event.ydata - 1)永远都是2
A:如果 y 的值在 (0, 1) 之间，确实会出现这个问题，因为 int() 函数会将小数部分舍去，而且 self.N 的值是整数，所以结果可能不如预期。为了解决这个问题，我们可以使用 np.floor() 或 np.ceil() 来确保正确地向下或向上取整。
……
x, y = int(event.xdata), int(np.floor(self.N - event.ydata - 1))
……

基本方向是对了，改的话就……emm。三次机会已到，不给它机会了。int()在非负取整结果上跟floor差不多，舍弃了浮点部分。GPT引用了numpy模块里的floor，也是常规用法吧，import math之后math.floor()也行。
关于int()与floor()，需要注意。int()对于负数而言会向“上”（向0）舍入到最接近的整数，而np.floor()总是向下舍入。np.floor()（来自numpy）能够对数组批量操作。

y = -1.1
print(np.floor(y),int(y))

output: -2.0 -1

就是GPT的表述，有点模糊吧，也放出来：（因为GPT表述太迷糊，上面的测试代码是自己写的）

int() 将向零舍入，因此对于正数，它会截取小数部分；而对于负数，它会向下舍入到最接近的整数。
np.floor() 总是向下舍入到最接近的整数，即使是负数也是如此。

渐变色“消失”

对于“3. 坐标为（3，3）的格子翻转状态无法正确显示，虽然边框好像会变”这个问题，估计是前期让它“渐变色中心向四周扩散”时出错了。试着问问GPT：

Q:现在有一些格子的渐变色与其它的不一样？能否指出是为什么吗？
在原始的代码中，每个格子的渐变色是根据其到网格中心的距离来确定的，距离越远，渐变色越接近透明。但是在处理点击事件时，触发事件的格子及其相邻格子被翻转，这导致它们的渐变色也被重新计算，可能与其他格子的渐变色不同。因此，触发事件的格子和相邻格子的渐变色可能会与其他格子不一样。
为了解决这个问题，我们可以在处理点击事件时，不重新计算触发事件格子的渐变色，而是保持它们的渐变色与原始状态相同。这样可以确保触发事件的格子及其相邻格子的渐变色与其他格子保持一致。

看来必须研究渐变色的代码了。另外，在目前的程序中，游戏一旦完成，点击事件的监听就被断开了，reset之后不会恢复对点击事件的监听，需要修改。

Q:请介绍这段代码涉及的函数：
self.ax.imshow(gradient, aspect=’auto’, extent=(j, j + 1, self.N - i - 1, self.N - i),cmap=self.cmap, alpha=alpha) # 绘制渐变色格子
Q:能否精简函数参数的介绍，尽量各用几个短语介绍
A:当然可以：

• gradient: 渐变色数组，表示从白色到指定颜色的渐变。
• aspect='auto': 自动调整图形的纵横比。
• extent=(j, j + 1, self.N - i - 1, self.N - i): 定义图像的范围。
• cmap=self.cmap: 指定用于颜色映射的 colormap。
• alpha=alpha: 控制图像的透明度。

与之前版本的代码对比，发现是这段代码的效果

distance = np.sqrt((i - self.N / 2) ** 2 + (j - self.N / 2) ** 2)  # 计算到网格中心的距离
alpha = max(0, min(1, distance / (self.N / 2)))  # 限制 alpha 在 0 到 1 的范围内

看来GPT对我的从中心到四周的渐变有些误解……估计就是alpha=0了。调alpha有效果，但是整体很不美观。还是得试试搞好渐变色。为了不受已有代码影响，我开了新对话。
与GPT拉扯了许久，下面是最终有效的提问

Q:import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColorma 请问可以用这两个画出哪些形状的渐变色？
Q:如何用LinearSegmentedColorma画出一个颜色从中心开始，由深蓝向紫晶蓝渐变的矩形？
Q:能否改为由天蓝渐变为深蓝再渐变为紫晶蓝
Q:如何将现在的自定义颜色覆盖到这段代码中？ ……
Q:能否将# Fill in the rectangle with gradient colors
for i in range(height):
for j in range(width):
# Calculate distance from center
distance = np.sqrt((j - center_x) ** 2 + (i - center_y) ** 2)
# Normalize distance to range [0, 1]
normalized_distance = distance / np.sqrt(center_x ** 2 + center_y ** 2)
# Map normalized distance to colormap
color = cmap(normalized_distance)
image[i, j] = color
return image
这段代码融入。注意，目的是让每个格子都能应用到这段你代码。需要对这段代码进行一些修改。

经过拉扯，最终的结果是这样的：012.py

好歹在N值大的时候能接受吧。不过当N为偶数时会逼死强迫症，不对称。但还是想试试之前的想法。

Q:我的意思是，每个格子都像之前的单个矩形一样，在单个格子内渐变

拉扯失败，自己改吧。017.py是期待的效果，但效果也不好。并且那段代码(018.py)是以像素为单位的。得深刻理解。先放一放。现在就做出了可用的游戏界面。另外再修改一下移除监视的部分。回到前面的那个对话。

reset的逻辑

Q:现在如果游戏被完成，按reset后也无法重新开始游戏
A:……
修正坐标转换：
x, y = int(event.xdata), int(self.N - event.ydata - 1) # 获取点击位置并转换 y 坐标

我可真谢谢你，给我改回错的版本了。把那个错误修正后，测试（020.py），现在完成后reset后仍然可以正常游戏了。
接下来，先添加记录步数的功能吧。代码越堆越多，可能会受到GPT输出长度限制。

Q:能否在屏幕上显示当前玩家操作的次数；并记录玩家完成游戏的历史最小次数。
Q:请生成完整代码
Q:请继续生成
Q:请注意：on_click中的x, y = int(event.xdata), int(self.N - event.ydata - 1)需改成x, y = int(event.xdata), int(self.N - event.ydata)

（021.py）运行过程中，文本框虽然不会被修改，但是会吸附焦点。试了一下，看起来GPT改不了(022.py)，直接把文本框改没了。先不管了。

可解题目的生成

现在需求3、4已经完成了，也就是界面内容已经完成了。剩下的主要是翻转游戏游戏性的拓展。
需求主要有： 1. 在游戏开始时随机一到两个格子处于翻转状态；该功能应该可以选择打开或关闭；reset也应该有“重试”或“获得新题目”的区分。 2. 题解：穷举剪枝（
为了在生成后可获取可行解，先实现题解的生成。但“对于这样一个程序，请添加’查看题解的功能‘”在前面问貌似不符合GPT的实现逻辑。还是得先生成初始态。

Q:能否添加一个设置菜单，其中可以选择reset后是否生成一个有两个格子被随机翻转的谜题，或是重置回目前的谜题的初始状态。

生成谜题与求解

现在可以生成初始两个被翻转的随机谜题，但是无法重现谜题的初始版图。

Q:勾选Randomize后，点击Reset，会生成随机的谜题（记为谜题1）；要求： 此时取消勾选Randomize，点击Reset之后，需要重现谜题1 。请进行修改 。 没有修改的代码部分不用给出。
GPT:
修改说明：
在类初始化方法中增加 self.random_puzzle 变量，用于存储当前生成的随机谜题状态。
在 reset_grid 方法中，当复选框被勾选并生成随机谜题后，将随机谜题状态存储到 self.random_puzzle。
在 reset_grid 方法中，当复选框未勾选时，检查 self.random_puzzle 是否不为 None，如果不为 None，恢复到上次生成的随机谜题状态，否则恢复到初始状态。
output:024.py （我才不会说是我忘记复制，直接把刚才那版覆盖了……）
这次GPT达到的我的目的，要继续修改应该比较容易。之后便是探索解集。
Q:能否添加一个功能：添加一个“获得答案”的按钮，按下之后可以生成答案。答案指：使得完成游戏需要点击的最少方格的各个方格的位置。用一个小的N*N板块显示。
output:025.py
Q:请给出具体的解决谜题的算法
output:026.py

026.py无法处理无解的谜题，会直接报错，

Q:Traceback (most recent call last):
……
TypeError: ‘NoneType’ object is not subscriptable 这有可能是因为问题无解
output:027.py
修改说明：
在 show_answer 方法中增加了对 solution 是否为 None 的检查。如果 solution 为 None，则打印 “No solution found.”。
在 solve_puzzle 方法的最后，如果没有找到解决方案，则返回 None。
通过这些修改，当没有解时，不会尝试显示 None，而是会输出一条消息。

目前的界面是这样的：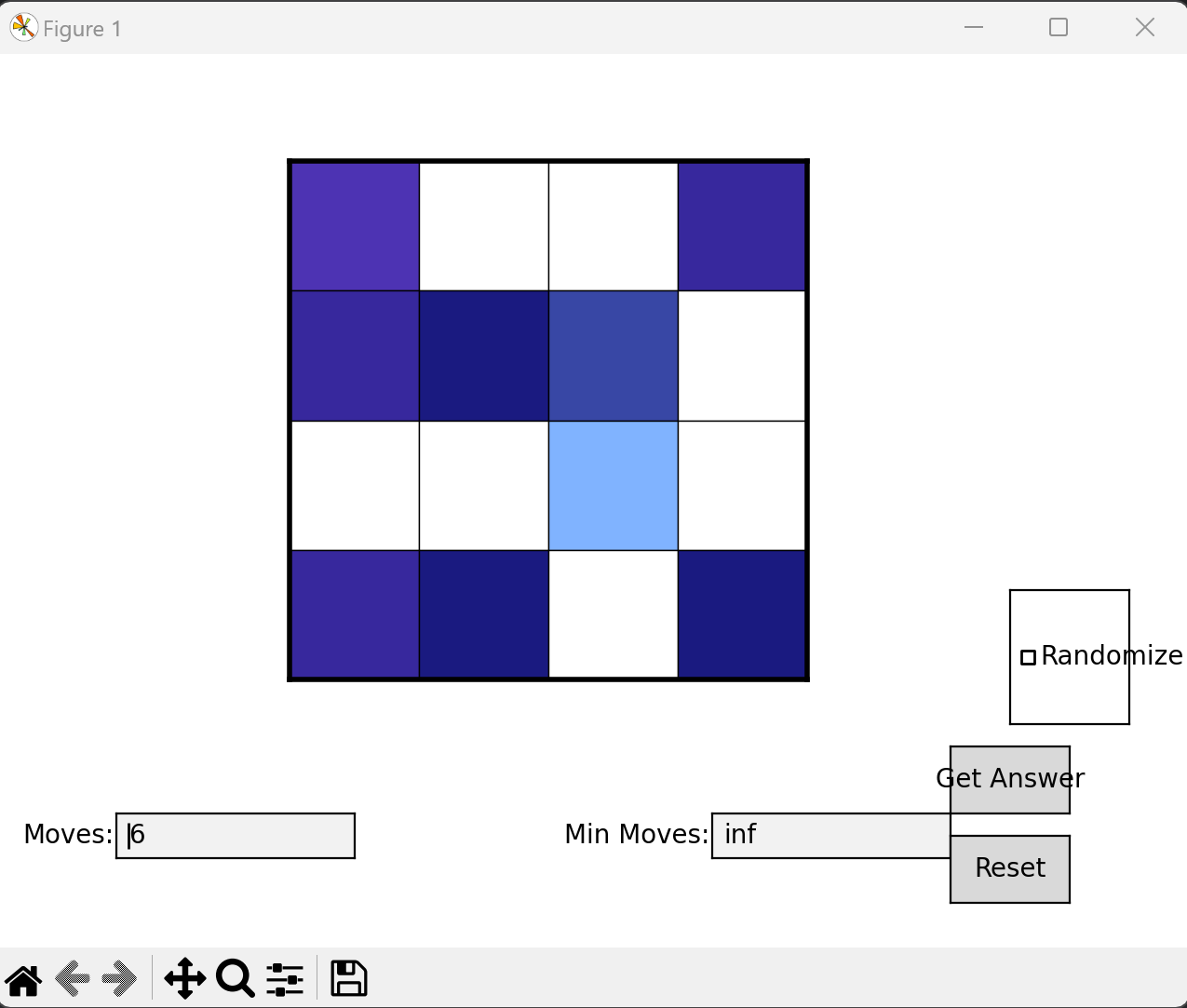

点击”Get Answer”按钮后: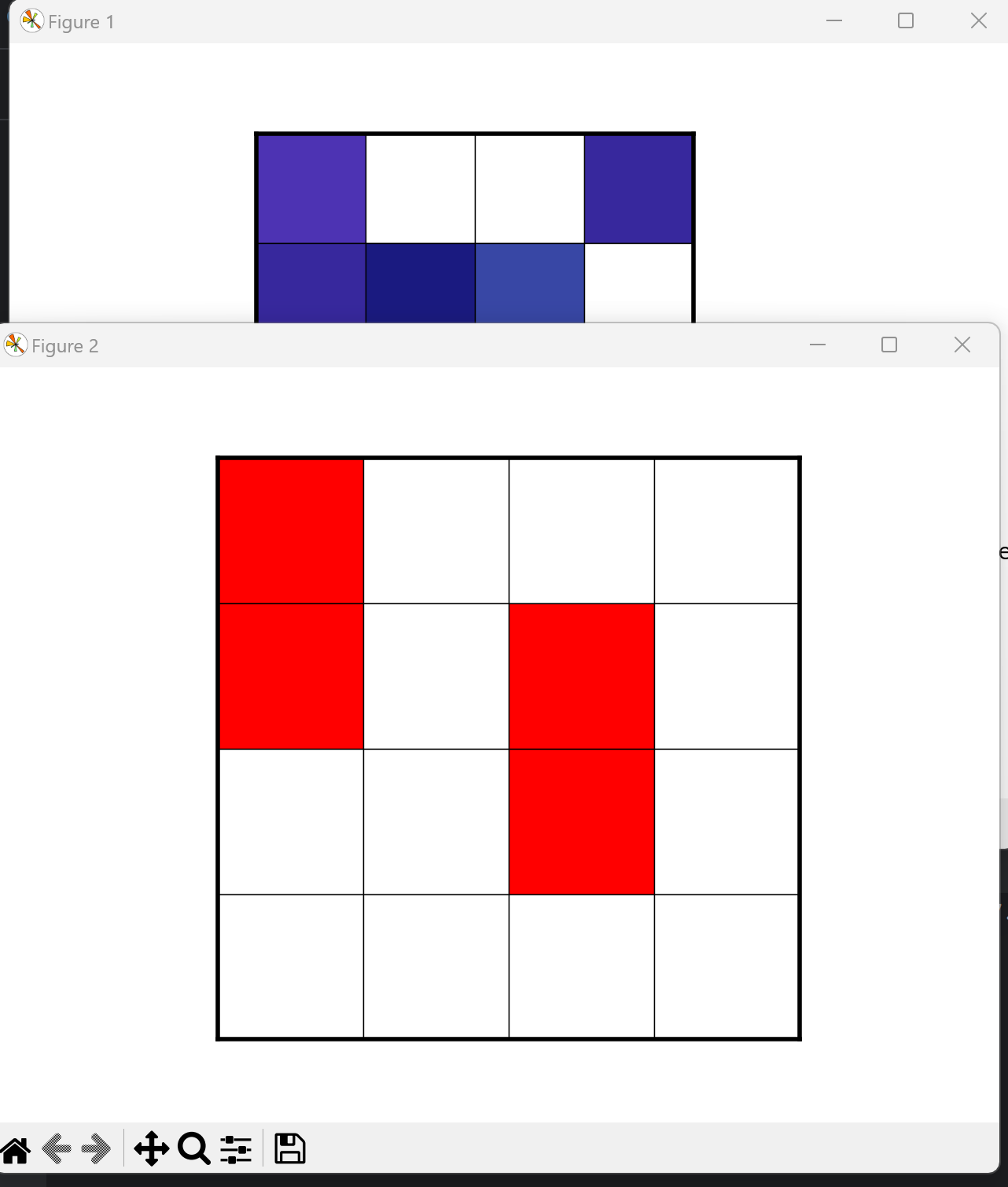

看起来，初始时若是2个格子被翻转，没有可行解。

Q:如何修改勾选Randomize后随机翻转的格子数？能否帮我改成3？
A:当然可以。你需要修改 randomize_grid 方法，使其在勾选 Randomize 后翻转三个随机的格子，而不是两个。
这里是修改后的代码片段：

class FlipGame:
    def __init__(self, N=4):
        # 初始化代码省略，保持不变

    # 其余代码省略，保持不变

    def randomize_grid(self):
        indices = np.random.choice(self.N * self.N, 3, replace=False)  # 选择 3 个随机的格子
        for index in indices:
            x, y = index // self.N, index % self.N
            self.grid[x, y] = not self.grid[x, y]

    # 其余代码省略，保持不变

这个修改将 randomize_grid 方法中的 np.random.choice 函数的参数改为 3，从而选择 3 个随机格子进行翻转。其余的代码保持不变。这样，勾选 Randomize 后点击 Reset 按钮，将会有三个随机的格子被翻转。

通过提问，我了解了它随机初始化的逻辑。要点就是形成一个(x,y)的元组，之后通过

self.grid[x, y] = not self.grid[x, y]

一句，将所有指定的坐标对于的格子翻转。理解这点后，我新建了一个对话，探讨翻转游戏的可行解。

可行解的探索

Q:对于4*4的翻转游戏，什么时候有解？
Q:能否写出一个或多个函数，（共同）实现生成可行谜题的代码 output：029可行解.py
Q:这段代码运行地太慢了。能否适当剪枝？ output:030可行解.py

现在得到了可以运行的初始谜题生成代码，原理是随机初始化点击行为：点击行为对格子状态的影响是可逆的。相比随机格子状态，这算是个生成可解谜题的好方法。
接下来就拿着这段代码让GPT融合。

Q:能否将下面这段代码融入到产生初始解的函数中？原来的函数功能如有冲突，请将其覆盖。 import numpy as np…….
output: 031.py

现在随机谜题的效果挺让我满意的。4*4时平均点4-5下。但修改N后，Get_Answer就崩了。

Q:当N不等于4时，Get_Answer会崩溃。请修改生成函数或者Get_Answer函数的逻辑，使其能正常运行
output:032.py

看起来，不能奢望GPT能写出解决翻转问题的代码(033.py系列)。因此032.py是暂时的可以产出4*4以内范围谜题与解决方案的程序。现在需求1、2也算是有限制地完成了（N<=4）。搞一搞UI美化吧。基于032.py版本。

Q:这段代码的UI很丑，包括但不限于渐变色不对称且对比度大；按钮排列不规律；文本框都是由被选中的光标等等问题，请尝试进行修改，并告诉我改了什么？

经过多次修改，UI的最终版面是这样的：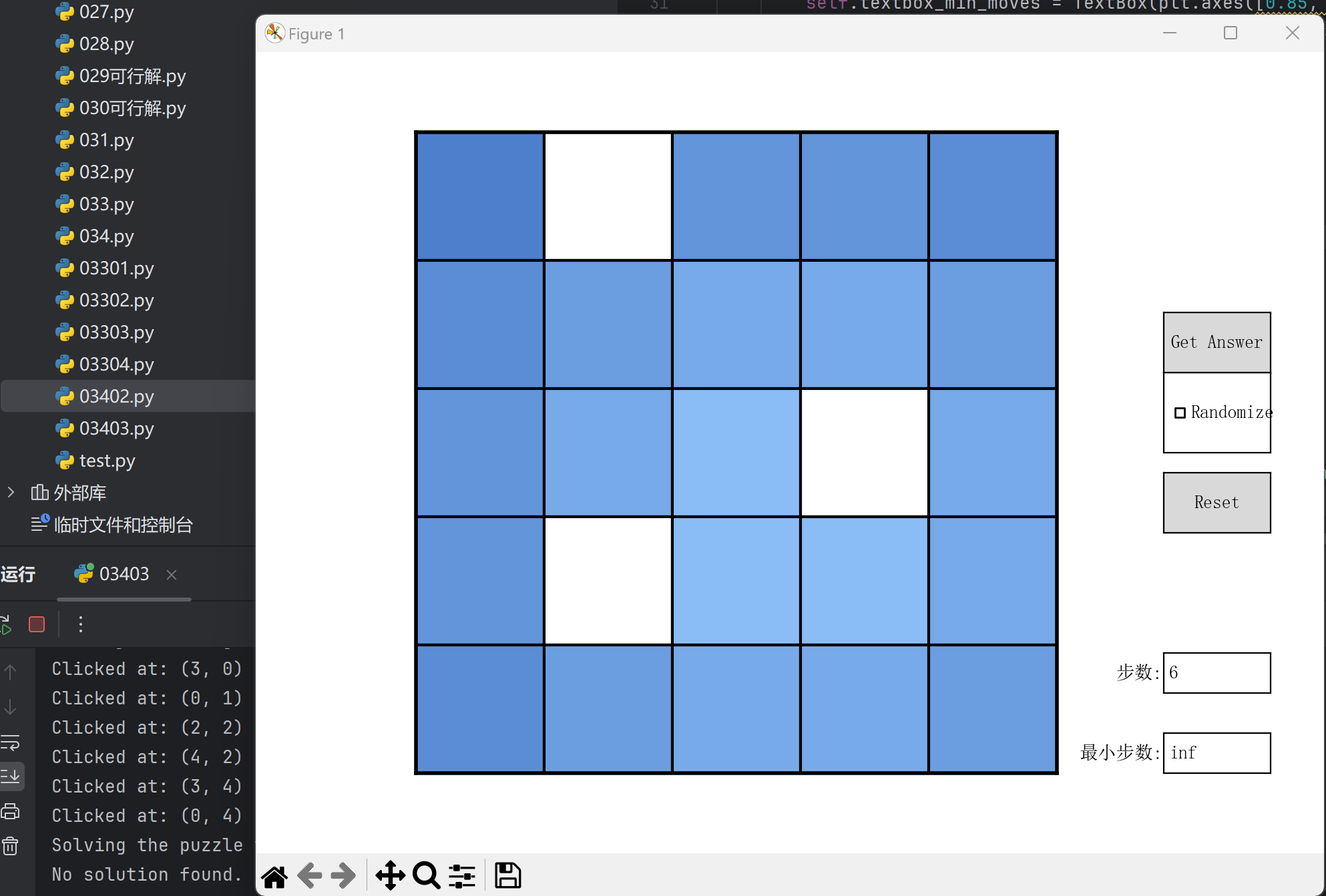

最终版本03404.py
这个项目就先到此结束了。
之后看一看要不要重启。

---

24/6/7
针对Filp_Game的解题算法，这几天做了多次搜索。理论可以暴力搜索，但是时间复杂度高（且我僵尸都打了四个多小时，真不会暴力）。我搜索到了一个解题的文章。变色方块(Flip Game)解法与可视化（我真感动，时隔快一个学期，我打出的a标签还是正确格式，其实md语法是这样：变色方块(Flip Game)解法与可视化）。这篇文章中利用了前人的研究，给出了使用高斯消元法对翻转问题求解的思路。我的理解是：对翻转游戏中的每一个格子都列一个线性方程，其中只自身与上下左右对应的xi置为1，’+’定义为异或。对于初始全零的初始状态，线性方程等号右边都是1。高斯消元法解线性方程组的过程，就是将矩阵化为阶梯矩阵，之后再求解。（线性代数相关内容）
这种数学逻辑还是得靠自己理解。GPT只有有限的数学处理能力。探索理解解题方法，也算是人不可被GPT替代的部分。
GPT成功帮我把求解的代码与原有程序融合。但是，只在初始全0状态时给出正确结果。经过多次提问修正，仍然不能给出能够求解有初始状态游戏的程序。
假定格子有0、1两种状态。翻转游戏的目标是让所有格子处于1状态。在线性方程中目标状态为1，可以理解为需要通过翻转，把对应格子的状态改变。当初始状态为全0时，所有格子都需要从0变为1，因此目标矩阵是全1的矩阵。一般情况，对于初始状态为1的格子，该格子的状态并不用改变，因此在目标矩阵的对应位置应该设置为0。极端情况，初始状态已经是全1，此时目标矩阵应该是全0，也就是要在操作后保持所有格子原有状态均不变。
主要涉及更改的函数如下：
(最终文件：107可用.py)

def show_answer(self, event):
    solution = self.solve_puzzle(self.grid)
    if solution is not None:
        self.display_solution(solution)
    else:
        print("No solution found.")

def solve_puzzle(self, grid):
    n = self.N
    a = []  # 异或方程组存在这里

    # 构建异或方程组
    for i in range(n):
        for j in range(n):
            d = np.zeros([n, n], np.int8)
            d[i][j] = 1
            if i != 0:
                d[i - 1][j] = 1
            if i != n - 1:
                d[i + 1][j] = 1
            if j != 0:
                d[i][j - 1] = 1
            if j != n - 1:
                d[i][j + 1] = 1
            a.append(d.flatten())

    a = np.array(a)
    b = np.ones(n * n, np.int8)  # 目标状态

    # 根据初始状态修改b矩阵，若初始状态为True，则不需要改变。
    # 根据高斯消元法，该格子异或的结果应该为0
    for i in range(n):
        for j in range(n):
            if grid[i][j]:
                b[i * n + j] ^= 1  # 可以直接置0，异或1也一样

    a = np.hstack((a, b[:, np.newaxis]))

    n2 = n * n
    line = 0
    # 高斯消元法解异或方程组
    for k in range(n2):
        for j in range(line, n2):
            if a[j][k] == 1:
                break
        if a[j][k] == 0:
            continue
        temp1, temp2 = np.copy(a[j]), np.copy(a[line])
        a[line], a[j] = temp1, temp2

        for i in range(line + 1, n2):
            if a[i][k] == 1:
                for j in range(k, n2 + 1):
                    a[i][j] = a[i][j] ^ a[line][j]
        line += 1
    for j in range(n2 - 1, -1, -1):
        for i in range(j):
            if a[i][j] == 1:
                a[i][n2] = a[i][n2] ^ a[j][n2]

    result = a[:, -1].reshape((n, n))
    solution_grid = np.zeros((n, n), dtype=bool)
    for i in range(n):
        for j in range(n):
            if result[i, j] == 1:
                solution_grid[i, j] = True
    return solution_grid

附重新启动前的源码：

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.colors as mcolors
from matplotlib.widgets import Button, TextBox, CheckButtons
from collections import deque
import time

plt.rcParams['font.sans-serif'] = ['SimSun', 'Microsoft YaHei']  # 设置中文字体


class FlipGame:
    def __init__(self, N=5):
        self.N = N
        self.grid = np.zeros((N, N), dtype=bool)
        self.initial_grid = self.grid.copy()
        self.random_puzzle = None
        self.colors = [(0.6, 0.8, 1.0), (0.3, 0.5, 0.8)]  # 调整颜色为柔和的蓝色渐变
        self.cmap = mcolors.LinearSegmentedColormap.from_list('custom_cmap', self.colors, N=256)
        self.num_moves = 0
        self.min_moves = float('inf')

        self.fig = plt.figure(figsize=(8, 6))
        self.ax = self.fig.add_subplot(111)  # 将游戏区域的高度调整为与按钮和选项框相匹配

        # 调整游戏区域的位置
        self.ax.set_position([0.1, 0.1, 0.7, 0.8])

        self.textbox_moves = TextBox(plt.axes([0.85, 0.2, 0.1, 0.05]), '步数:', initial=str(self.num_moves))
        self.textbox_moves.color = 'white'  # 设置文本框背景颜色

        self.textbox_min_moves = TextBox(plt.axes([0.85, 0.1, 0.1, 0.05]), '最小步数:', initial=str(self.min_moves))
        self.textbox_min_moves.color = 'white'  # 设置文本框背景颜色

        reset_ax = plt.axes([0.85, 0.4, 0.1, 0.075])
        self.reset_button = Button(reset_ax, 'Reset')  # 修改按钮边框颜色
        self.reset_button.on_clicked(self.reset_grid)

        check_ax = plt.axes([0.85, 0.5, 0.1, 0.1])
        self.check_button = CheckButtons(check_ax, ['Randomize'], [False])

        answer_ax = plt.axes([0.85, 0.6, 0.1, 0.075])
        self.answer_button = Button(answer_ax, 'Get Answer')  # 修改按钮边框颜色
        self.answer_button.on_clicked(self.show_answer)

        self.draw_grid()

        self.cid = self.fig.canvas.mpl_connect('button_press_event', self.on_click)

    def reset_grid(self, event):
        if self.check_button.get_status()[0]:
            self.grid = self.generate_solvable_puzzle()
            self.random_puzzle = self.grid.copy()
        else:
            if self.random_puzzle is not None:
                self.grid[:] = self.random_puzzle
            else:
                self.grid[:] = self.initial_grid

        self.num_moves = 0
        self.update_moves_text()
        self.draw_grid()
        self.cid = self.fig.canvas.mpl_connect('button_press_event', self.on_click)

    def draw_grid(self):
        self.ax.clear()
        self.ax.set_xticks([])
        self.ax.set_yticks([])
        for spine in self.ax.spines.values():
            spine.set_linewidth(2)
        for i in range(self.N):
            for j in range(self.N):
                if self.grid[i, j]:
                    color = self.calculate_color(j, i)
                    rect = plt.Rectangle([j, self.N - i - 1], 1, 1, facecolor=color, edgecolor='black', linewidth=1.5)  # 增加边框宽度
                    self.ax.add_patch(rect)
                else:
                    rect = plt.Rectangle([j, self.N - i - 1], 1, 1, facecolor='white', edgecolor='black', linewidth=1.5)  # 增加边框宽度
                    self.ax.add_patch(rect)
        self.ax.set_xlim(0, self.N)
        self.ax.set_ylim(0, self.N)
        self.ax.set_aspect('equal')
        self.fig.canvas.draw()

    def calculate_color(self, x, y):
        center_x = self.N / 2
        center_y = self.N / 2
        distance = np.sqrt((x - center_x) ** 2 + (y - center_y) ** 2)
        normalized_distance = distance / np.sqrt(center_x ** 2 + center_y ** 2)
        return self.cmap(normalized_distance)

    def update_moves_text(self):
        self.textbox_moves.set_val(str(self.num_moves))

    def update_min_moves_text(self):
        self.textbox_min_moves.set_val(str(self.min_moves))

    def on_click(self, event):
        if event.inaxes != self.ax:
            return
        x, y = int(event.xdata), int(self.N - event.ydata)
        print(f"Clicked at: ({x}, {y})")
        self.flip_tile(x, y)
        self.num_moves += 1
        self.update_moves_text()
        self.draw_grid()
        if np.all(self.grid):
            print("Congratulations! You win!")
            self.min_moves = min(self.min_moves, self.num_moves)
            self.update_min_moves_text()
            self.fig.canvas.mpl_disconnect(self.cid)

    def flip_tile(self, x, y):
        for dx, dy in [(0, 0), (0, 1), (0, -1), (1, 0), (-1, 0)]:
            nx, ny = x + dx, y + dy
            if 0 <= nx < self.N and 0 <= ny < self.N:
                self.grid[ny, nx] = not self.grid[ny, nx]

    def show_answer(self, event):
        solution = self.solve_puzzle(self.grid)
        if solution is not None:
            self.display_solution(solution)
        else:
            print("No solution found.")

    def solve_puzzle(self, grid, max_duration=5):
        def flip(grid, x, y):
            for dx, dy in [(0, 0), (0, 1), (0, -1), (1, 0), (-1, 0)]:
                nx, ny = x + dx, y + dy
                if 0 <= nx < self.N and 0 <= ny < self.N:
                    grid[nx, ny] = not grid[nx, ny]

        initial_state = grid.copy()
        target_state = np.ones((self.N, self.N), dtype=bool)

        queue = deque([(initial_state, [])])
        visited = set()
        start_time = time.time()

        while queue:
            if time.time() - start_time > max_duration:
                print("Solving the puzzle took too long.")
                return None

            current_grid, path = queue.popleft()
            if np.array_equal(current_grid, target_state):
                solution_grid = np.zeros((self.N, self.N), dtype=bool)
                for x, y in path:
                    solution_grid[x, y] = True
                return solution_grid
            state_tuple = tuple(map(tuple, current_grid))
            if state_tuple in visited:
                continue
            visited.add(state_tuple)

            for i in range(self.N):
                for j in range(self.N):
                    new_grid = current_grid.copy()
                    flip(new_grid, i, j)
                    new_path = path + [(i, j)]
                    queue.append((new_grid, new_path))

        return None

    def display_solution(self, solution):
        fig, ax = plt.subplots()
        ax.set_xticks([])
        ax.set_yticks([])
        for spine in ax.spines.values():
            spine.set_linewidth(2)
        for i in range(self.N):
            for j in range(self.N):
                if solution[i, j]:
                    rect = plt.Rectangle([j, self.N - i - 1], 1, 1, facecolor='red', edgecolor='black', linewidth=1.5)  # 增加边框宽度
                    ax.add_patch(rect)
                else:
                    rect = plt.Rectangle([j, self.N - i - 1], 1, 1, facecolor='white', edgecolor='black', linewidth=1.5)  # 增加边框宽度
                    ax.add_patch(rect)
        ax.set_xlim(0, self.N)
        ax.set_ylim(0, self.N)
        ax.set_aspect('equal')
        plt.show()

    def generate_solvable_puzzle(self):
        def flip(board, i, j):
            n = len(board)
            board[i, j] ^= 1
            if i > 0:
                board[i - 1, j] ^= 1
            if i < n - 1:
                board[i + 1, j] ^= 1
            if j > 0:
                board[i, j - 1] ^= 1
            if j < n - 1:
                board[i, j + 1] ^= 1

        n = self.N
        board = np.zeros((n, n), dtype=bool)

        num_flips = np.random.randint(1, n * n + 1)
        flips = np.random.choice(n * n, num_flips, replace=False)

        for flip_index in flips:
            i, j = divmod(flip_index, n)
            flip(board, i, j)
        return board
# 创建和显示游戏界面
flip_game = FlipGame()
plt.show()